This section is dealing with specific types of analysis performed by MDANSE. If you are not sure where these fit into the general workflow of data analysis, please read Workflow of the Analysis.

11. Analysis: Scattering

This section discusses plugins used to calculate neutron spectroscopy observables from the trajectory. These plugins will be explored in depth in further sections, however, before that, it is important to understand how MDANSE performs these analyses. A part of that are Q vectors, which are used to perform these analyses. An in-depth discussion of this aspect is present in Appendix 2.

11.1. Theory and background

The quantity of interest in neutron scattering experiments with thermal neutrons is the dynamic structure factor, S(q, 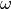$\omega$ ), which is closely related to the double differential cross-section [7], ${d^{2}{\sigma/\mathit{d\Omega dE}}}$ . The double differential cross section is defined as the number of neutrons which are scattered per unit time into the solid angle interval ${\left\lbrack {\Omega,{\Omega + d}\Omega} \right\rbrack}$ and into the energy interval ${{\lbrack{E,{E + \mathit{dE}}}\rbrack}}$ . It is normalized to d, dE, and the flux of the incoming neutrons,

(11.1) ${{\frac{d^{2}\sigma}{d\Omega\mathit{dE}} = N}\cdot\frac{k}{k_{0}}S\left( {q,\omega} \right).}$

Here N is the number of atoms, and k ≡ |k| and k₀ ≡ |k₀| are the wave numbers of scattered and incident neutrons, respectively. They are related to the corresponding neutron energies by

(11.2) ${E = \hslash^{2}}k^{2}\text{/}2m$

and

(11.3) ${E_{0} = \hslash^{2}}k_{0}^{2}\text{/}2m$

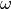where $m$ is the neutron mass. The arguments of the dynamic structure factor, $q$ and $\omega$ , are the momentum and energy transfer in units of $\hslash$ , respectively:

(11.4) ${{q = \frac{k_{0} - k}{\hslash}},}$

(11.5) ${{\omega = \frac{E_{0} - E}{\hslash}}.}$

The modulus of the momentum transfer can be expressed in the scattering angle $\theta$ , the energy transfer, and the energy of the incident neutrons:

(11.6) ${{q = \sqrt{{2 - \frac{\mathit{\hslash\omega}}{E_{0}} - 2}\cos{\theta\sqrt{2 - \frac{\mathit{\hslash\omega}}{E_{0}}}}}}.}$

The dynamic structure factor contains information about the structure and dynamics of the scattering system [Ref16]. It can be written as

(11.7) ${S{\left( {q,\omega} \right) = \frac{1}{2\pi}}{\int\limits_{- \infty}^{+ \infty}\mathit{dt}}\exp\left\lbrack {{- i}\omega t} \right\rbrack F\left( {q,t} \right).}$

F(q, t) is called the intermediate scattering function and is defined as

(11.8) ${\text{F}{\left( {q,t} \right) = {\sum\limits_{\alpha,\beta}{\Gamma_{\mathit{\alpha\beta}}\left\langle {\exp\left\lbrack {{- i}q\cdot\hat{R_{\alpha}}(0)} \right\rbrack\exp\left\lbrack {iq\cdot\hat{R_{\beta}}(t)} \right\rbrack} \right\rangle}}},}$

(11.9) ${{\Gamma_{\mathit{\alpha\beta}} = \frac{1}{N}}\left\lbrack {\overline{b_{\alpha}}{\overline{b_{\beta}} + \delta_{\mathit{\alpha\beta}}}\left( {\overline{b_{\alpha}^{2}} - {\overline{b_{\alpha}}}^{2}} \right)} \right\rbrack.}$

The operators $\hat{R_{\alpha}}(t)$ in Eq. (11.8) are the position operators of the nuclei in the sample. The brackets $\langle\ldots\rangle$ denote a quantum thermal average and the time dependence of the position operators is defined by the Heisenberg picture. The quantities $b_{\alpha}$ are the scattering lengths of the nuclei which depend on the isotope and the relative orientation of the spin of the neutron and the spin of the scattering nucleus. If the spins of the nuclei and the neutron are not prepared in a special orientation one can assume a random relative orientation and that spin and position of the nuclei are uncorrelated. The symbol $\overline{...}$ appearing in ${\Gamma_{\mathit{\alpha\beta}}}$ denotes an average over isotopes and relative spin orientations of neutron and nucleus.

Usually, one splits the intermediate scattering function and the dynamic structure factor into their coherent and incoherent parts which describe collective and single particle motions, respectively. Defining

(11.10) ${b_{\alpha,\mathit{coh}}\doteq\overline{b_{\alpha}},}$

(11.11) ${b_{\alpha,\mathit{inc}}\doteq\sqrt{\overline{b_{\alpha}^{2}} - {\overline{b_{\alpha}}}^{2}},}$

the coherent and incoherent intermediate scattering functions can be cast in the form

(11.12) ${\text{F}_{\text{coh}}{\left( {q,t} \right) = \frac{1}{N}}{\sum\limits_{\alpha,\beta}b_{\alpha,\mathit{coh}}}b_{\beta,\mathit{coh}}\left\langle {\exp\left\lbrack {{- i}q\cdot\hat{R_{\alpha}}(0)} \right\rbrack\exp\left\lbrack {iq\cdot\hat{R_{\beta}}(t)} \right\rbrack} \right\rangle,}$

(11.13) ${\text{F}_{\text{inc}}{\left( {q,t} \right) = \frac{1}{N}}{\sum\limits_{\alpha}{b_{\alpha,\mathit{inc}}^{2}\left\langle {\exp\left\lbrack {{- i}q\cdot\hat{R_{\alpha}}(0)} \right\rbrack\exp\left\lbrack {iq\cdot\hat{R_{\alpha}}(t)} \right\rbrack} \right\rangle}}.}$

Rewriting these formulas, MDANSE introduces the partial terms as:

(11.14) ${\text{F}_{\text{coh}}{\left( {q,t} \right) = \sum\limits_{I,J\geq I}^{N_{\mathit{species}}}}\sqrt{n_{I}n_{J}\omega_{I,\text{coh}}\omega_{J,\text{coh}}}F_{\mathit{IJ},\text{coh}}\left( {q,t} \right),}$

(11.15) ${\text{F}_{\text{inc}}{\left( {q,t} \right) = {\sum\limits_{I = 1}^{N_{\mathit{species}}}{n_{I}\omega_{I,\text{inc}}F_{I,\text{inc}}\left( {q,t} \right)}}}}$

where:

(11.16) ${\text{F}_{\mathit{IJ},\text{coh}}{\left( {q,t} \right) = \frac{1}{\sqrt{n_{I}n_{J}}}}{\sum\limits_{\alpha}^{n_{I}}{\sum\limits_{\beta}^{n_{J}}\left\langle {\exp\left\lbrack {{- i}q\cdot\hat{R_{\alpha}}\left( t_{0} \right)} \right\rbrack\exp\left\lbrack {iq\cdot\hat{R_{\beta}}\left( {t_{0} + t} \right)} \right\rbrack} \right\rangle_{t_{0}}}},}$

(11.17) ${\text{F}_{I,\text{inc}}{\left( {q,t} \right) = \frac{1}{n_{I}}}{\sum\limits_{\alpha = 1}^{n_{I}}\left\langle {\exp\left\lbrack {{- i}q\cdot\hat{R_{\alpha}}\left( t_{0} \right)} \right\rbrack\exp\left\lbrack {iq\cdot\hat{R_{\alpha}}\left( {t_{0} + t} \right)} \right\rbrack} \right\rangle_{t_{0}}}.}$

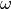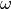where n_I, n_J, N_species, $\omega$ _I,coh,inc and $\omega$ _J,coh,inc are defined in Section Coordination Number.

The corresponding dynamic structure factors are obtained by performing the Fourier transformation defined in Eq. (11.7).

An important quantity describing structural properties of liquids is the static structure factor, which is defined as

(11.18) ${\text{S}(q)\doteq{\int\limits_{- \infty}^{+ \infty}{d\omega}}\text{S}_{\mathit{coh}}\left( {q,\omega} \right)\text{F}_{\mathit{coh}}\left( {q,0} \right).}$

In the classical framework the intermediate scattering functions are interpreted as classical time correlation functions. The position operators are replaced by time-dependent vector functions and quantum thermal averages are replaced by classical ensemble averages. It is well known that this procedure leads to a loss of the universal detailed balance relation,

(11.19) ${\text{S}{\left( {q,\omega} \right) = \exp}\left\lbrack {\beta\hslash\omega} \right\rbrack\text{S}\left( {{- q}{, - \omega}} \right),}$

and also to a loss of all odd moments

(11.20) ${\left\langle \omega^{2{n + 1}} \right\rangle\doteq{\int\limits_{- \infty}^{+ \infty}{d\omega}}\omega^{2{n + 1}}S\left( {q,\omega} \right),{n = 1,2},\ldots.}$

The odd moments vanish since the classical dynamic structure factor is even in 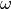$\omega$ , assuming invariance of the scattering process with respect to reflections in space. The first moment is also universal. For an atomic liquid, containing only one sort of atoms, it reads

(11.21) ${{\left\langle \omega \right\rangle = \frac{\hslash q^{2}}{2M}},}$

where M is the mass of the atoms. Formula (11.21) shows that the first moment is given by the average kinetic energy (in units of $\hslash$ ) of a particle which receives a momentum transfer $\hslash q$ . Therefore, $\langle\omega\rangle$ is called the recoil moment. A number of ‘recipes’ has been suggested to correct classical dynamic structure factors for detailed balance and to describe recoil effects in an approximate way. The most popular one has been suggested by Schofield [Ref17]

(11.22) ${{\text{S}\left( {q,\omega} \right)\approx\exp\left\lbrack \frac{\beta\hslash\omega}{2} \right\rbrack}_{}\text{S}_{\mathit{cl}}\left( {q,\omega} \right)}$

One can easily verify that the resulting dynamic structure factor fulfils the relation of detailed balance. Formally, the correction (11.22) is correct to first order in $\hslash$ . Therefore, it cannot be used for large q-values which correspond to large momentum transfers $\hslash q$ . This is actually true for all correction methods which have suggested so far. For more details we refer to Ref. [Ref18].

MDANSE computes the partial S(Q)’s as the Fourier transform of the partial g(r), corresponding to the Faber-Ziman definition:

(11.23) ${S_{\alpha\beta}(Q) = 1 + \frac{4\pi\rho_0}{Q}\int\limits_{0}^{\infty}{r\left\lbrack {g_\alpha\beta}(r)-1 \right\rbrack\text{sin}(Qr)dr}}$

The total S(Q) is computed as a weighted sum similar to the one used for the total g(r). In the case of the analysis ‘X-ray Static structure factor’, the Q-dependence of the atomic form factors is taken into account in this weighted sum.

Again, Soper has provided experimental data (table 4 in ISRN Physical Chemistry, 279463 (2013), given in file soper13_fx.dat). Here a source of confusion is that the data can be normalized in different ways (see Soper’s paper). Using the normalization II in that reference we have that:

(11.24) ${D_{x}{(Q) = \frac{\sum\limits_{\mathit{\alpha\beta}\geq\alpha}{\left( {2 - \delta_{\mathit{\alpha\beta}}} \right)\times c_{\alpha}c_{\beta}f_{\alpha}{(Q)}f_{\beta}{(Q)}\left\lbrack {S_{\mathit{\alpha\beta}}{(Q) - 1}} \right\rbrack}}{\sum\limits_{\alpha}{c_{\alpha}f_{\alpha}^{2}{(Q)}}} = \left\lbrack {S{(Q) - 1}} \right\rbrack}\times\frac{\sum\limits_{\mathit{\alpha\beta}}{c_{\alpha}c_{\beta}f_{\alpha}{(Q)}f_{\beta}{(Q)}}}{\sum\limits_{\alpha}{c_{\alpha}f_{\alpha}^{2}{(Q)}}}}$

Where S(Q) would be the static structure factor (going to 1 at large Q) computed by MDANSE. Therefore, even after using MDANSE we should recalculate the x-ray observable using the atomic factors.

11.2. Current Correlation Function

11.2.1. Theory and implementation

Current correlation function is typically used to study the propagation of excitations in disordered systems. In MDANSE, its longitudinal and transverse components are calculated, which are related to density fluctuations and propagating shear modes respectively. Formalism and other details can be found in Ref [Ref19].

11.2.2. GUI

available for trajectories only

Frames
Instrument resolution
Interpolation order
interpolation mode (only applicable when interpolation order is set to something different than ‘no interpolation’)

Format: str

Default: automatic

Description: the method that will be used to interpolate velocities. All modes give identical results but differ in speed and memory usage. The following modes are available:

one-time in-memory interpolation

In this mode, all velocities are interpolated once, at the beginning, and stored in memory. This mode is the fastest but requires large amounts of memory. It is recommended for use with small trajectories. When used with large trajectories, it is advisable that a computer with sufficient memory is used.

repeated interpolation

In this mode, all velocities are interpolated in each loop over Q-shells. Therefore, it is slower, though less memory is required. However, the largest memory usage depends on the composition of the sample; it is most efficient when all elements have equal number of particles in the sample, and the least when one element has the majority of particles. Thus, it is advisable that this mode is used with medium trajectories with even distribution of elements, especially when the computer has only an HDD. When used with large trajectories, please ensure that the computer has sufficient memory.

one-time disk interpolation

In this mode, all velocities are interpolated once, at the beginning, and stored on disk. This makes it slow but with little memory requirement. This balance of speed and memory can be further altered by using the ‘number of preloaded frames’ option. This mode is meant for when the computer has insufficient memory for the other modes and is advisable to be used with large trajectories. Further, since disk is involved, it is advisable that the computer has an SSD, and that the operating system’s temp folder is on that disk.

automatic

In this mode, MDANSE selects one of the above modes to be used that should be best given the hardware. It does this by estimating the memory requirements and comparing them to the total memory of the computer.

number of preloaded frames (only applicable when ‘interpolation mode’ is set to ‘one-time disk interpolation)

Format: int

Default: 50

Description: this option allows for the optimisation of the ‘one-time disk interpolation’ interpolation mode. It governs the number of frames for which the velocities are loaded from disk to memory at once. Thus, if it is set to 1, the interpolated velocities of all particles are loaded into memory one frame at a time, and if it is 50, 50 frames worth of interpolated velocities are loaded, and then no loading occurs for the next 49 frames, after which the next 50 are loaded. This way, the speed and memory usage can be adjusted; the larger the number, the faster (though with diminishing returns) but the more memory required.

Please note that this option can be set to a value of -1, which will cause all the interpolated velocities for all the particles of one element to be loaded into memory at once. This way, the memory usage is comparable to the ‘repeated interpolation’ interpolation mode. Further, when SSD is used, the analysis can be faster than in the ‘repeated interpolation’ mode.

11.3. Dynamic Coherent Structure Factor

11.3.1. Theory and implementation

Please refer to Theory and background for more details about the theoretical background related to the dynamic coherent structure factor. In this analysis, MDANSE proceeds in two steps. First, it computes the partial and total intermediate coherent scattering function using equation (11.14). Then, the partial and total dynamic coherent structure factors are obtained by performing the Fourier Transformation, defined in Eq. (11.7), respectively on the total and partial intermediate coherent scattering functions.

MDANSE computes the coherent intermediate scattering function on a rectangular grid of equidistantly spaced points along the time-and the q-axis, respectively:

(11.25) ${{F}_{\text{coh}}\left( {q_{m},k\cdot\Delta t} \right)\doteq{\sum\limits_{{I = 1},J\geq I}^{N_{\mathit{species}}}\sqrt{n_{I}n_{J}\omega_{I,\text{com}}\omega_{I,\text{com}}}}{\overline{\left\langle {\rho_{I}\left( {{-q},0} \right)\rho_{J}\left( {q,k\cdot\Delta t} \right)} \right\rangle}}^{q},} \\ {{k = 0}\ldots{N_{t} - 1},{m = 0}\ldots{N_{q} - 1.}}$

where N_t is the number of time steps in the coordinate time series, N_q is a user-defined number of q-shells, N_species is the number of selected species, n_I the number of atoms of species I, 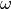$\omega$ _I the weight for species I (see Section Coordination Number for more details) and ${\rho_{I}\left( {q,k\cdot\Delta t} \right)}$ is the Fourier transformed particle density for species I defined as

(11.26) ${\rho_{I}{\left( {q,k\cdot\Delta t} \right) = \sum\limits_{\alpha}^{n_{I}}}\exp\left\lbrack {\mathit{iq}\cdot R_{\alpha}\left( {k\cdot\Delta t} \right)} \right\rbrack.}$

The symbol ${\overline{...}}^{q}$ in Eq. (11.25) denotes an average over q-vectors having approximately the same modulus

(11.27) ${{q_{m} = {q_{\mathit{\min}} + m}}\cdot\Delta q}$

. The particle density must not change if jumps in the particle trajectories due to periodic boundary conditions occur. In addition, the average particle density, $N/V$ , must not change. This can be achieved by choosing q-vectors on a lattice which is reciprocal to the lattice defined by the MD box. Let b₁, b₂, b₃ be the basis vectors which span the MD cell. Any position vector in the MD cell can be written as

(11.28) ${{R = x^{'}}{b_{1} + y^{'}}{b_{2} + z^{'}}b_{3},}$

with x’, y’, z’ having values between 0 and 1. The primes indicate that the coordinates are box coordinates. A jump due to periodic boundary conditions causes x’, y’, z’ to jump by $\pm1$ . The set of dual basis vectors b¹, b², b³ is defined by the relation

(11.29) ${b_{i}{b^{j} = \delta_{i}^{j}}.}$

If the q-vectors are now chosen as

(11.30) ${{q = 2}\pi\left( {k{b^{1} + l}{b^{2} + m}b^{3}} \right),}$

where k,l,m are integer numbers, jumps in the particle trajectories produce phase changes of multiples of $2\pi$ in the Fourier transformed particle density, i.e. leave it unchanged. One can define a grid of q-shells or a grid of q-vectors along a given direction or on a given plane, giving in addition a tolerance for q. MDANSE looks then for q-vectors of the form given in Eq. 61 whose moduli deviate within the prescribed tolerance from the equidistant q-grid. From these q-vectors only a maximum number per grid-point (called generically q-shell also in the anisotropic case) is kept.

The q-vectors can be generated isotropically, anisotropically or along user-defined directions. The $\sqrt{\omega_{I}}$ may be negative if they represent normalized coherent scattering lengths, i.e.

(11.31) ${{\sqrt{\omega_{I}} = \frac{b_{I,\text{coh}}}{\sqrt{\sum\limits_{I = 1}^{N_{\mathit{species}}}{n_{I}b_{I,\text{coh}}^{2}}}}}.}$

Negative coherent scattering lengths occur in hydrogenous materials since $b_{\mathit{coh},H}$ is negative [Ref20]. The density-density correlation is computed via the FCA technique described in the section The FCA algorithm.

When the default value of weights ( $b_{coherent}$ ) is chosen for this analysis, the result will correspond to that of the equation (11.63) from the Neutron Dynamic Total Structure Factor.

11.3.2. GUI

available for trajectories only

11.4. Dynamic Incoherent Structure Factor

11.4.1. Theory and implementation

Please refer to Theory and background section for more details about the theoretical background related to the dynamic incoherent structure factor. In this analysis, MDANSE proceeds in two steps. First, it computes the partial and total intermediate incoherent scattering function F_inc(q, t) using equation (11.14). Then, the partial and total dynamic incoherent structure factors are obtained by performing the Fourier Transformation, defined in Eq. (11.7), respectively on the total and partial intermediate incoherent scattering function.

MDANSE computes the incoherent intermediate scattering function on a rectangular grid of equidistantly spaced points along the time-and the q-axis, respectively:

(11.32) ${\text{F}_{\text{inc}}\left( {q_{m},k\cdot\Delta t} \right)\doteq{\sum\limits_{I = 1}^{N_{\mathit{species}}}{n_{I}\omega_{I,\text{inc}}}}\text{F}_{I,\text{inc}}\left( {q_{m},k\cdot\Delta t} \right),\\ {k = 0}\ldots{N_{t} - 1},{m = 0}\ldots{N_{q} - 1.}}$

where N_t is the number of time steps in the coordinate time series, N_q is a user-defined number of q-shells, N_species is the number of selected species, n_I the number of atoms of species I, 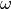$\omega$ _I the weight for species I (see Section Coordination Number for more details) and ${F_{I,\text{inc}}\left( {q_{m},k\cdot\Delta t} \right)}$ is defined as:

(11.33) ${\text{F}_{I,\mathit{inc},\alpha}{\left( {q_{m},k\cdot\Delta t} \right) = \sum\limits_{\alpha = 1}^{n_{I}}}{\overline{\left\langle {\exp\left\lbrack {{-i}q\cdot R_{\alpha}(0)} \right\rbrack\exp\left\lbrack {iq\cdot R_{\alpha}(t)} \right\rbrack} \right\rangle}}^{q}.}$

The symbol ${\overline{...}}^{q}$ in Eq. (11.33) denotes an average over q-vectors having approximately the same modulus ${{q_{m} = {q_{\mathit{\min}} + m}}\cdot\Delta q}$ . The particle density must not change if jumps in the particle trajectories due to periodic boundary conditions occur. In addition, the average particle density, N/V, must not change. This can be achieved by choosing q-vectors on a lattice which is reciprocal to the lattice defined by the MD box. Let b₁, b₂, b₃ be the basis vectors which span the MD cell. Any position vector in the MD cell can be written as

(11.34) ${{R = x^{'}}{b_{1} + y^{'}}{b_{2} + z^{'}}b_{3},}$

with x’, y’, z’ having values between 0 and 1. The primes indicate that the coordinates are box coordinates. A jump due to periodic boundary conditions causes x’, y’, z’ to jump by $\pm 1$ . The set of dual basis vectors b¹, b², b³ is defined by the relation

(11.35) ${b_{i}{b^{j} = \delta_{i}^{j}}.}$

If the q-vectors are now chosen as

(11.36) ${{q = 2}\pi\left( {k{b^{1} + l}{b^{2} + m}b^{3}} \right),}$

where k,l,m are integer numbers, jumps in the particle trajectories produce phase changes of multiples of 2π in the Fourier transformed particle density, i.e. leave it unchanged. One can define a grid of q-shells or a grid of q-vectors along a given direction or on a given plane, giving in addition a tolerance for q. MDANSE looks then for q-vectors of the form given in Eq. (11.36) whose moduli deviate within the prescribed tolerance from the equidistant q-grid. From these q-vectors only a maximum number per grid-point (called generically q-shell also in the anisotropic case) is kept.

The q-vectors can be generated isotropically, anisotropically or along user-defined directions.

The correlation functions defined in (11.33) are computed via the FCA technique described in the section The FCA algorithm. Although the efficient FCA technique is used to compute the atomic time correlation functions, the program may consume a considerable amount of CPU-time since the number of time correlation functions to be computed equals the number of atoms times the total number of q-vectors. This analysis is actually one of the most time-consuming among all the analysis available in MDANSE.

When the default value of weights ( ${b^{2}}_{incoherent}$ ) is chosen for this analysis, the result will correspond to that of the equation (11.64) from the Neutron Dynamic Total Structure Factor.

11.4.2. GUI

available for trajectories only

11.5. Elastic Incoherent Structure Factor

11.5.1. Theory and implementation

The Elastic Incoherent Structure Factor (EISF) is defined as the limit of the incoherent intermediate scattering function for infinite time,

(11.37) ${\mathit{EISF}(q)\doteq\lim\limits_{t\rightarrow\infty}\text{F}_{\mathit{inc}}\left( {q,t} \right).}$

Using the above definition of the EISF one can decompose the incoherent intermediate scattering function as follows:

(11.38) ${\text{F}_{\text{inc}}{\left( {q,t} \right) = \mathit{EISF}}{(q) + \text{F}_{\text{inc}}^{'}}\left( {q,t} \right),}$

where F_inc‘(q,t) decays to zero for infinite time. Taking now the Fourier transform it follows immediately that

(11.39) ${\text{S}_{\text{inc}}{\left( {q,\omega} \right) = \mathit{EISF}}(q)\delta{(\omega) + \text{S}_{\text{inc}}^{'}}\left( {q,\omega} \right).}$

The EISF appears as the amplitude of the elastic line in the neutron scattering spectrum. Elastic scattering is only present for systems in which the atomic motion is confined in space, as for solids. To understand which information is contained in the EISF we consider for simplicity a system where only one sort of atoms is visible to the neutrons. To a very good approximation this is the case for all systems containing a large amount of hydrogen atoms, as biological systems. Incoherent scattering from hydrogen dominates by far all other contributions. Using the definition of the van Hove self-correlation function G_s(r, t) [Ref20],

(11.40) ${b_{\text{inc}}^{2}G_{s}\left( {r,t} \right)\doteq\frac{1}{2\pi^{3}}{\int d^{3}}q\exp\left\lbrack {{- i}q\cdot r} \right\rbrack\text{F}_{\mathit{inc}}\left( {q,t} \right),}$

which can be interpreted as the conditional probability to find a tagged particle at the position r at time t, given it started at r = 0, one can write:

(11.41) ${\mathit{EISF}{(q) = b_{\text{inc}}^{2{\int d^{3}}}}r\exp\left\lbrack {\mathit{iq}\cdot r} \right\rbrack G_{s}\left( {r,{t = \infty}} \right).}$

The EISF gives the sampling distribution of the points in space in the limit of infinite time. In a real experiment this means times longer than the time which is observable with a given instrument. The EISF vanishes for all systems in which the particles can access an infinite volume since G_s(r, t) approaches 1/V for large times. This is the case for molecules in liquids and gases.

For computational purposes it is convenient to use the following representation of the EISF [Ref21]:

(11.42) ${\mathit{EISF}{(q) = {\sum\limits_{I = 1}^{N_{\mathit{species}}}{n_{I}\omega_{I,\text{inc}}\mathit{EIS}F_{I}(q)}}}}$

where N_species is the number of selected species, n_I the number of atoms of species I, 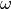$\omega$ _I,inc the weight for species I (see Section Coordination Number for more details) and for each species the following expression for the elastic incoherent scattering function is

(11.43) ${\mathit{EIS}F_{I}{(q) = \frac{1}{n_{I}}}{\sum\limits_{\alpha}^{n_{I}}\left\langle {|{\exp\left\lbrack {\mathit{iq}\cdot R_{\alpha}} \right\rbrack\left. {} \right|^{2}}} \right\rangle}.}$

This expression is derived from definition (11.37) of the EISF and expression (11.15) for the intermediate scattering function, using that for infinite time the relation

(11.44) ${\left\langle {\mathit{ex}p\left\lbrack {{- \mathit{iq}}\cdot R_{\alpha}(0)} \right\rbrack\mathit{ex}p\left\lbrack {\mathit{iq}\cdot R_{\alpha}(t)} \right\rbrack} \right\rangle = \left\langle {|{\mathit{ex}p\left\lbrack {\mathit{iq}\cdot R_{\alpha}} \right\rbrack\left. {} \right|^{2}}} \right\rangle}$

holds. In this way the computation of the EISF is reduced to the computation of a static thermal average. We remark at this point that the length of the MD trajectory from which the EISF is computed should be long enough to allow for a representative sampling of the conformational space.

MDANSE allows one to compute the elastic incoherent structure factor on a grid of equidistantly spaced points along the q-axis:

(11.45) ${\mathit{EISF}\left( q_{m} \right)\doteq{\sum\limits_{I = 1}^{N_{\mathit{species}}}{n_{I}\omega_{I}\mathit{EIS}F_{I}\left( q_{m} \right)}},{m = 0}\ldots{N_{q} - 1.}}$

where N_q is a user-defined number of q-shells, the values for q_m are defined as

(11.46) ${{q_{m} = {q_{\mathit{\min}} + m}}\cdot\Delta q}$

, and for each species the following expression for the elastic incoherent scattering function is:

(11.47) ${\mathit{EIS}F_{I}{\left( q_{m} \right) = \frac{1}{n_{I}}}{\sum\limits_{\alpha}^{n_{I}}{\overline{\left\langle {|{\exp\left\lbrack {\mathit{iq}\cdot R_{\alpha}} \right\rbrack\left. {} \right|^{2}}} \right\rangle}}^{q}}.}$

Here the symbol ${\overline{...}}^{q}$ denotes an average over the q-vectors having the same modulus q_m. The program corrects the atomic input trajectories for jumps due to periodic boundary conditions.

11.5.2. GUI

available for trajectories only

11.6. Gaussian Dynamic Incoherent Structure Factor

11.6.1. Theory and implementation

The MSD can be related to the incoherent intermediate scattering function via the cumulant expansion [Ref11], [Ref22]

(11.48) ${\text{F}_{\text{inc}}^{g}{\left( {q,t} \right) = {\sum\limits_{I = 1}^{N_{\mathit{species}}}{n_{I}\omega_{I,\text{inc}}}}}\text{F}_{I,\text{inc}}^{g}\left( {q,t} \right)}$

where N_species is the number of selected species, n_I the number of atoms of species I, 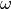$\omega$ _I,inc the weight for species I (see Section Coordination Number for more details) and

(11.49) ${\text{F}_{I,\text{inc}}^{g}{\left( {q,t} \right) = \frac{1}{n_{I}}}\sum\limits_{\alpha}^{n_{I}}\exp\left\lbrack {{- q^{2}}\rho_{\alpha,1}{(t) + q^{4}}\rho_{\alpha,2}(t)\mp\ldots} \right\rbrack.}$

The cumulants

(11.50) ${\rho_{\alpha,k}(t)}$

are identified as

(11.51) ${\rho_{\alpha,1}{(t) = \left\langle {d_{\alpha}^{2}\left( {t;n_{q}} \right)} \right\rangle}}$

(11.52) ${\rho_{\alpha,2}{(t) = \frac{1}{4!}}\left\lbrack {{\left\langle {d_{\alpha}^{4}\left( {t;n_{q}} \right)} \right\rangle - 3}\left\langle {d_{\alpha}^{2}\left( {t;n_{q}} \right)} \right\rangle^{2}} \right\rbrack}$

${\vdots}$

The vector nq is the unit vector in the direction of q. In the Gaussian approximation the above expansion is truncated after the q²-term. For certain model systems like the ideal gas, the harmonic oscillator, and a particle undergoing Einstein diffusion, this is exact. For these systems the incoherent intermediate scattering function is completely determined by the MSD. MDANSE allows one to compute the total and partial incoherent intermediate scattering function in the Gaussian approximation by discretizing equation (11.48):

(11.53) ${\text{F}_{\text{inc}}^{g}\left( {q_{m},k\cdot\Delta t} \right)\doteq{\sum\limits_{I = 1}^{N_{\mathit{species}}}{n_{I}\omega_{I,\text{inc}}\text{F}_{I,\text{inc}}^{g}\left( {q_{m},k\cdot\Delta t} \right)}},{k = 0}\ldots{N_{t} - 1},{m = 0}\ldots{N_{q} - 1.}}$

with for each species the following expression for the intermediate scattering function:

(11.54) ${\text{F}_{I,\alpha,\text{inc}}^{g}{\left( {q_{m},k\cdot\Delta t} \right) = \frac{1}{n_{I}}}\sum\limits_{\alpha}^{n_{I}}\exp\left\lbrack {\frac{- \left( q_{m} \right)^{2}}{6}\Delta_{\alpha}^{2}\left( {k\cdot\Delta t} \right)} \right\rbrack\mathit{isotropic}\mathit{system}}$

(11.55) ${\text{F}_{I,\alpha,\text{inc}}^{g}{\left( {q_{m},k\cdot\Delta t} \right) = \frac{1}{n_{I}}}\sum\limits_{\alpha}^{n_{I}}\exp\left\lbrack {\frac{- \left( q_{m} \right)^{2}}{2}\Delta_{\alpha}^{2}\left( {k\cdot\Delta t;n} \right)} \right\rbrack\mathit{isotropic}\mathit{system}}$

N_t is the total number of time steps in the coordinate time series and N_q is a user-defined number of q-shells. The (q, t)-grid is the same as for the calculation of the intermediate incoherent scattering function (see Dynamic Incoherent Structure Factor). The quantities

(11.56) ${\Delta_{\alpha}^{2}(t)}$

and

(11.57) ${\Delta_{\alpha}^{2}\left( {t;n} \right)}$

are the mean-square displacements, defined in Equations (10.6) and (10.7), respectively. They are computed by using the algorithm described in the Mean Square Displacement section. MDANSE corrects the atomic input trajectories for jumps due to periodic boundary conditions. It should be noted that the computation of the intermediate scattering function in the Gaussian approximation is much ‘cheaper’ than the computation of the full intermediate scattering function, F_inc(q, t), since no averaging over different q-vectors needs to be performed. It is sufficient to compute a single mean-square displacement per atom.

11.6.2. GUI

available for trajectories only

11.7. Neutron Dynamic Total Structure Factor

available for trajectories only

This is a combination of the Dynamic Coherent and the Dynamic Incoherent Structure Factors. It is a fully neutron-specific analysis, where the coherent part of the intermediate scattering function is calculated using the atomic coherent neutron scattering lengths $b_{coherent}$ and the incoherent one is calculated using the square of the atomic incoherent neutron scattering lengths ${b^{2}}_{incoherent}$ . Therefore, in this analysis the weights option is not available.

The partial coherent intermediate scattering functions $I_{\alpha\beta}^{coh}(Q,t)$ (and their corresponding Fourier transforms giving the partial coherent dynamic structure factors, $S_{\alpha\beta}^{coh}(Q,\omega)$ ) are calculated exactly in the same way as in the DCSF analysis, i.e.:

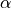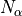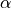(11.58) $I_{\alpha\beta}^{coh}(Q,t) = \left| \frac{1}{\sqrt{N_{\alpha}N_{\beta}}}\sum_{i \in \alpha,j \in \beta}^{N_{\alpha},N_{\beta}}\left\langle e^{- i\mathbf{Q}\mathbf{r}_{i}(t_{0})}e^{i\mathbf{Q}\mathbf{r}_{j}(t_{0} + t)} \right\rangle \right|_{\mathbf{Q}}$

where $\alpha$ and $\beta$ refer to the chemical elements, $N_{\alpha}$ and $N_{\beta}$ are the respective number of atoms of each type, $i$ and $j$ are two specific atoms of type $\alpha$ and $\beta$ , respectively, and $\mathbf{r}_{i}(0)$ and $\mathbf{r}_{j}(t)$ are their positions at the time origin and at the time $t$ , respectively. The notation $\left\langle \ldots \right\rangle$ indicates an average over all possible time origins $t_{0}$ and $|\ldots|_{\mathbf{Q}}$ represents an average over all the $\mathbf{Q}$ vectors contributing to the corresponding $Q$ -bin.

Similarly, the partial incoherent intermediate scattering functions $I_{\alpha}^{inc}(Q,t)$ and the partial incoherent dynamic structure factors $S_{\alpha}^{inc}(Q,\omega)$ are obtained as in the DISF analysis:

(11.59) $I_{\alpha}^{inc}(Q,t) = \left| \frac{1}{N_{\alpha}}\sum_{i \in \alpha}^{N_{\alpha}}\left\langle e^{- i\mathbf{Q}\mathbf{r}_{i}(t_{0})}e^{i\mathbf{Q}\mathbf{r}_{i}(t_{0} + t)} \right\rangle \right|_{\mathbf{Q}}$

The main difference between this analysis and the DCSF and DISF analyses, apart from the fact that the coherent and incoherent contributions are calculated simultaneously, is the way the different partial contributions are combined. In this analysis the total incoherent, total coherent and total (coherent + incoherent) signals are calculated as:

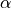(11.60) $I^{inc}(Q,t) = \sum_{\alpha}^{N_{\alpha}}{c_{\alpha}b_{\alpha,\text{inc}}^{2}}I_{\alpha}^{inc}(Q,t)$

(11.61) $I^{coh}(Q,t) = \sum_{\alpha,\beta}^{N_{\alpha},N_{\beta}}{\sqrt{c_{\alpha}c_{\beta}}b_{\alpha,\text{coh}}b_{\beta,\text{coh}}I_{\alpha\beta}^{coh}(Q,t)}$

(11.62) $I^{tot}(Q,t) = I^{inc}(Q,t) + I^{coh}(Q,t) = \sum_{\alpha}^{N_{\alpha}}{c_{\alpha}b_{\alpha,\text{inc}}^{2}}I_{\alpha}^{inc}(Q,t) + \sum_{\alpha,\beta}^{N_{\alpha},N_{\beta}}{\sqrt{c_{\alpha}c_{\beta}}b_{\alpha,\text{coh}}b_{\beta,\text{coh}}I_{\alpha\beta}^{coh}(Q,t)}$

where $c_{\alpha} = \frac{N_{\alpha}}{N}$ and $c_{\beta} = \frac{N_{\beta}}{N}$ are the concentration numbers for elements $\alpha$ and $\beta$ , respectively.

These expressions correspond to the formalism and equations given in [Ref47], chapter 1: “An introduction to neutron scattering” .

As in the MDANSE database the coherent and incoherent neutron scattering lengths are given in Å, the total intermediate scattering functions above will be given in Å²/sterad/atom. Therefore, multiplying the output from MDANSE by a factor 10⁸ we can obtain these neutron observables in barn/sterad/atom and compare them directly to the experimental results (assuming the later have been properly normalized and presented in absolute units).

On the other hand, the DISF and DCSF analyses use the standard weight normalization procedure implemented in MDANSE (see Normalize). Therefore the total coherent intermediate scattering function returned by the DCSF analysis is (assuming that the chosen weights are b_coherent):

(11.63) $I^{coh}(Q,t) = \frac{\sum_{\alpha\beta}^{n}{c_{\alpha}c_{\beta}b_{\alpha,coh}b_{\beta,coh}I_{\alpha\beta}^{coh}(Q,t)}}{\sum_{\alpha\beta}^{n}{c_{\alpha}c_{\beta}b_{\alpha,coh}b_{\beta,coh}}}$

And the incoherent intermedicate scattering function given by the DISF analysis is (assuming that the chosen weights are b_incoherent2):

(11.64) $I^{inc}(Q,t) = \frac{\sum_{\alpha}^{n}{c_{\alpha}b_{\alpha,inc}^{2}I_{\alpha}^{inc}(Q,t)}}{\sum_{\alpha}^{n}{c_{\alpha}b_{\alpha,inc}^{2}}}$

Naturally, similar expressions apply to the dynamic structure factors, $S_{\alpha\beta}^{coh}(Q,\omega)$ and $S_{\alpha}^{inc}(Q,\omega)$ .

11.8. Structure Factor From Scattering Function

available for analysis results only
- it appears in all analysis results, even for non-scattering analyses which cannot be used to compute this